
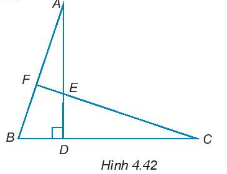
Cho 5 điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE
a) Chứng minh rằng AB = CE
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = {90^0}\)

a) Chứng minh \(\Delta DAB = \Delta DCE\left( {c - g - c} \right)\)
b) \(\Delta DAB = \Delta DCE\left( {cmt} \right) \Rightarrow \widehat {BAD} = \widehat {ECD}\)

Advertisements (Quảng cáo)
a)
Xét \(\Delta DAB\) và \(\Delta DCE\) có:
\(DA = DC\left( {gt} \right)\\\widehat {ADB} = \widehat {CDE} (= {90^0})\\DB = DE\left( {gt} \right)\\ \Rightarrow \Delta DAB = \Delta DCE\left( {c - g - c} \right)\)
\(\Rightarrow AB = CE\) ( 2 cạnh tương ứng)
b)
Ta có: \(\Delta DAB = \Delta DCE\left( {cmt} \right)\)
\(\Rightarrow \widehat {BAD} = \widehat {ECD}\) ( 2 góc tương ứng)
Do vậy :
\(\begin{array}{l}\widehat {BFC} = {180^0} - \widehat {FCB} - \widehat {CBF} = {180^0} - \widehat {ECD} - \widehat {DBA}\\\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - \widehat {BAD} - \widehat {DBA} = \widehat {ADB} = {90^0}\end{array}\)
Vậy \(\widehat {BFC} = {90^0}\)
