
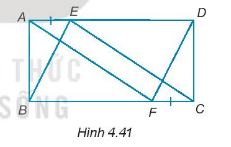
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy 2 điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
a)\(AF = CE\)
b)\(AF // CE\)

a)Chứng minh \(\Delta ABF = \Delta CDE\left( {c - g - c} \right)\)
b)Chứng minh 2 góc ở vị trí đồng vị bằng nhau.

Ta có: \(\left\{ \begin{array}{l}BF = BC - CF\\DE = DA - AE\end{array} \right. \Rightarrow BF = DE\).
Advertisements (Quảng cáo)
Xét \(\Delta ABF\) và \(\Delta CDE\) có:
BA = DC (2 cạnh đối hình chữ nhật)
\( BF = DE\).
\(\widehat B = \widehat D = {90^0}\)
\(\Rightarrow \Delta ABF = \Delta CDE\left( {c - g - c} \right)\)
\(\Rightarrow AF = CE\) ( 2 cạnh tương ứng)
b)
Ta có: \(\Delta ABF = \Delta CDE\left( {cmt} \right) \Rightarrow \widehat {AFB} = \widehat {DEC}\) ( 2 góc tương ứng)
Vì \(AD // BC \Rightarrow \widehat {DEC} = \widehat {ECB}\)(2 góc so le trong)
Do đó:\(\widehat {AFB} =\widehat {ECB}\). Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow AF // CE\) ( Dấu hiệu nhận biết 2 đường thẳng song song)
