
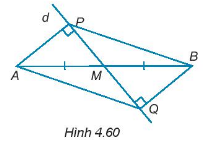
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ \(\left( {P \in d,Q \in d} \right)\)vuông góc với đường thẳng d (H 4.60). Chứng minh rằng:
a) AP = BQ
b)\(\Delta APB = \Delta BQA\).

a) Chứng minh: \(\Delta PAM = \Delta QBM\left( {ch - gn} \right)\)
b) Chứng minh theo trường hợp c – g – c.

a)
Advertisements (Quảng cáo)
Xét \(\Delta PAM\) vuông tại P và \(\Delta QBM\) vuông tại Q có:
AM = BM (gt)
\(\widehat {PMA} = \widehat {QMB}\) (2 góc đối đỉnh)
\(\begin{array}{l}\Rightarrow \Delta PAM = \Delta QBM\left( {ch - gn} \right)\end{array}\)
\( \Rightarrow AP = BQ\) (2 cạnh tương ứng)
b)
Xét \(\Delta APB\) và \(\Delta BQA\) có:
AP = BQ (cmt)
\(\widehat {PAB} = \widehat {QBA}\left( {\text{do} \Delta PAM = \Delta QBM} \right)\)
AB: Cạnh chung
\( \Rightarrow \Delta APB = \Delta BQA\left( {c - g - c} \right)\).
