Chứng minh rằng OE là tia phân giác của góc xOy.. Câu 29 trang 141 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
Cho góc xOy. Trên tia Ox lấy tâm điểm C, trên tia Oy lấy điểm D sao cho OD = OC. Vẽ các cung tròn tâm C và tâm D có cùng bán kính sao cho chúng cắt nhau ở điểm E nằm trong góc xOy. Chứng minh rằng OE là tia phân giác của góc xOy.

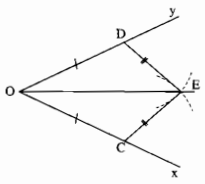
Xét ∆COE và ∆DOE, ta có:
OE cạnh chung
Advertisements (Quảng cáo)
OD = OC (bán kính của 1 cung tròn)
DE = CE (bán kính 2 cung tròn bằng nhau)
Suy ra: ∆COE = ∆DOE (c.c.c)
Vậy: \(\widehat {COE} = \widehat {DOE}\) (hai góc tương ứng)
Vì OE nằm giữa OC và OD nên OE là tia phân giác của góc DOC hay OE là tia phân giác góc xOy.
