Chứng minh rằng AD // BC.. Câu 34 trang 141 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính bằng BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau ở D (D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC.

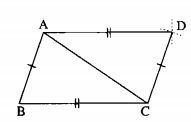
Xét ∆ABC và ∆CDA, ta có:
AB = CD (theo cách vẽ)
Advertisements (Quảng cáo)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: \(\Delta ABC{\rm{ }} = {\rm{ }}\Delta CDA{\rm{ }}\left( {c.c.c} \right) \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\)
Vậy: AD // BC (vì có cặp góc ở vị trí so le trong bằng nhau).
