Chứng minh rằng hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.. Câu 41 trang 44 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 5: Tính chất tia phân giác của một góc
Cho tam giác ABC. Chứng minh rằng hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.
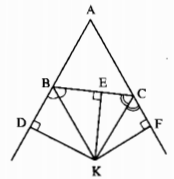
Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.
Kẻ \(KE \bot BC,KF \bot {\rm{A}}C,K{\rm{D}} \bot AB\)
Vì K nằm trên tia phân giác của \(\widehat {CB{\rm{D}}}\)
\( \Rightarrow \) KD = KE (tính chất tia phân giác) (1)
Advertisements (Quảng cáo)
Vì K nằm trên tia phân giác của \(\widehat {BCF}\)
\( \Rightarrow \) KE = KF (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: KD = KF
Điểm K nằm trong \(\widehat {BAC}\) cách đều 2 cạnh AB và AC
Điểm K nằm trên tia phân giác của \(\widehat {BAC}\)
Vậy đường phân giác trong của \(\widehat {A}\) đi qua K.