Cho đường thẳng AC và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.

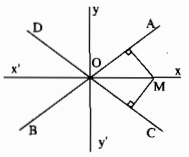
Xét M nằm trong góc AOC.
Kẻ \(MH \bot OA,MK \bot {\rm{O}}C\)
Xét hai tam giác vuông MHO và MKO:
\(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \)
MH = MK
OM cạnh huyền chung
Do đó ∆MHO = ∆MKO (cạnh huyền - …)
\( \Rightarrow \widehat {MOH} = \widehat {MOK}\) (2 góc tương ứng)
Advertisements (Quảng cáo)
=>OM là tia phân giác của \(\widehat {AOC}\)
Ngược lại, M nằm trên tia phân giác của \(\widehat {AOC}\)
Xét hai tam giác vuông MHO và MKO:
\(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \)
\(\widehat {MOH} = \widehat {MOK}\)
OM cạnh huyền chung
Do đó ∆MHO = ∆MKO (cạnh huyền – góc nhọn)
\( \Rightarrow \) MH = MK (2 cạnh tương ứng)
Vậy tập hợp các điểm M cách đều OA và OC là tia phân giác Ox của góc AOC.
Tương tự M nằm trong các góc AOD, DOB, BOC tập hợp các điểm M là tia phân giác Oy, Ox’, Oy’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
