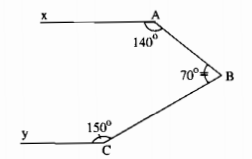
Hình dưới cho biết \(\widehat A = 140^\circ ;\widehat B = 70^\circ ;\widehat C = 150^\circ \)
Chứng minh rằng Ax // Cy

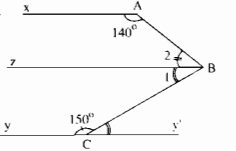
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: \(\widehat {{B_2}} + \widehat {xAB} = 180^\circ \) (hai góc trong cùng phía)
Mà \(\widehat {xAB} = 140^\circ (gt)\)
Suy ra: \(\widehat {{B_2}} = 180^\circ - \widehat {xAB}\)
Advertisements (Quảng cáo)
\( \Rightarrow \) \(\widehat {{B_2}} = 180^\circ - 140^\circ = 40^\circ \)
Mà \(\widehat {{B_1}} + \widehat {{B_2}} = \widehat {ABC}\)
\( \Rightarrow \widehat {{B_1}} = \widehat {ABC} - \widehat {{B_2}}\)
= 70° - 40° = 30° (1)
\(\widehat {yCB} + \widehat {BCy’} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {BCy’} = 180^\circ - \widehat {yCB} = 180^\circ - 150^\circ = 30^\circ (2)\)
Từ (1) và (2) suy ra: \(\widehat {{B_1}} = \widehat {BCy’}\)
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
