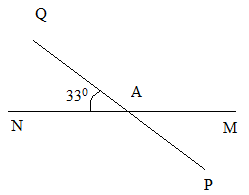
Hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo bằng \(33^\circ \).
a) Tính số đo góc NAQ.
b) Tính số đo góc MAQ.
c) Viết tên các cặp góc đối đỉnh.
d) Viết tên các cặp góc bù nhau.

a) Ta có:
\(\widehat {NAQ}\) và \(\widehat {PAM}\) là hai góc đối đỉnh
Advertisements (Quảng cáo)
Suy ra: \(\widehat {NAQ} = \widehat {PAM}\)
Mà \(\widehat {PAM} = 33^\circ \) nên \(\widehat {NAQ} = 33^\circ \)
b) \(\widehat {PAM}\) và \(\widehat {MAQ}\) là hai góc kề bù nên \(\widehat {PAM} + \widehat {MAQ} = 180^\circ \)
Suy ra: \(\widehat {MAQ} = 180^\circ - \widehat {PAM} = 180^\circ - 33^\circ = 147^\circ \)
c) Các cặp góc đối đỉnh là \(\widehat {PAM}\) và \(\widehat {NAQ}\); \(\widehat {PAN}\) và \(\widehat {MAQ}\)
d) Các cặp góc kề bù nhau là:
\(\widehat {PAM}\) và \(\widehat {MAQ}\); \(\widehat {PAM}\) và \(\widehat {PAN}\);
\(\widehat {NAQ}\) và \(\widehat {PAN}\); \(\widehat {NAQ}\) và \(\widehat {QAM}\).
