Câu 7.1 trang 48Sách Bài Tập (SBT) Toán lớp 7 tập 2
Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng?
\(\left( A \right)\widehat {AMN} \ne \widehat {BMN}\)
\(\left( B \right)\widehat {MAN} \ne \widehat {MBN}\)
\(\left( C \right)\widehat {MNA} \ne \widehat {MNB}\)
\(\left( D \right)\Delta AMN = \Delta BMN\)
Giải
Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB. Tương tự, NA = NB. Ta có ∆AMN = ∆BMN (c.c.c) nên các khẳng định (A), (B), (C) sai, (D) đúng.
Câu 7.2 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho hai tam giác cân chung đáy ABC và ABD, trong đó ABC là tam giác đều. Gọi E là trung điểm của AB. Khi đó, khẳng định nào sau đây là sai?
(A) Đường thẳng CD là đường trung trực của AB.
(B) Điểm E không nằm trên đường thẳng CD.
(C) Đường trung trực của AC đi qua B.
Advertisements (Quảng cáo)
(D) Đường trung trực của BC đi qua A.
Giải
Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB. Tương tự NA = NB. Ta có ∆AMN = ∆BMN (c.c.c) nên các khẳng định (A), (B), (C) sai và (D) đúng.
Đáp số (D) Đường trung trực của BC đi qua A.
Câu 7.3 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm:
a) AD và CD nếu BD = 5cm; AC = 8cm;
b) AC nếu BD = 11,4cm; AD = 3,2cm.
Giải
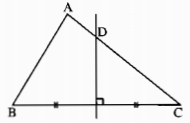
a) Vì D thuộc đường trung trực của BC nên DB = DC. Mặt khác, D ở giữa A và C nên AD = AC – DC
Nếu BD = 5cm; AC = 8cm, thì CD = BD = 5cm và AD = 8 – 5 = 3 (cm).
b) AC = AD + DC = AD + BD = 3,2 + 11,4 = 14,6 (cm).
