Câu 7.4 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:
a) D là trung điểm của cạnh BC.
b) \(\widehat A = \widehat B + \widehat C\)
Giải
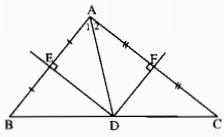
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có ∆DEB = ∆DEA(c.g.c) nên \(\widehat B = \widehat {{A_1}}\). Tương tự \(\widehat C = \widehat {{A_2}}\).
Suy ra \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\)
Câu 7.5 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC.
Advertisements (Quảng cáo)
Giải
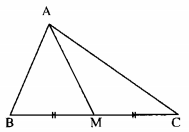
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử \(AM \bot BC\). Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra A = AC. Điều này mâu thuẫn với giả thiết AB # AC. Vậy trung tuyến AM không vuông góc với BC.
Câu 7.6 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đường thẳng d và hai điểm A, B nằm về một phía của d sao cho AB không vuông góc với d. Hãy tìm trên d một điểm M sao cho \(\left| {MA - MB} \right|\) có giá trị nhỏ nhất.
Giải
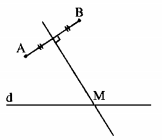
Ta có \(\left| {MA - MB} \right| \ge 0\) với một điểm M tùy ý và \(\left| {MA - MB} \right| = 0\) chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB.
Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d.
Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì \(\left| {MA - MB} \right|\) đạt giá trị nhỏ nhất và bằng 0.
