
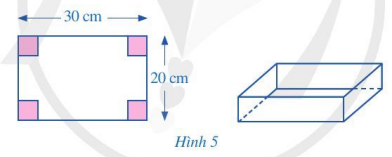
Từ tấm bìa hình chữ nhật có kích thước 20 cm và 30 cm, bạn Quân cắt đi ở mỗi góc của tấm bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh, sau đó gấp lại để tạo thành hình hộp chữ nhật không nắp (Hình 5). Viết đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi.

Thể tích của hình hộp chữ nhật bằng chiều dài nhân chiều rộng nhân chiều cao cùng đơn vị đo.
Đối với bài trên, chiều dài của hình hộp chữ nhật bằng chiều dài của tấm bìa sau khi cắt, chiều rộng của hình hộp chữ nhật bằng chiều rộng của tấm bìa sau khi cắt, chiều cao của hình hộp chữ nhật bằng độ dài của cạnh hình vuông cắt.
Advertisements (Quảng cáo)

Gọi độ dài cạnh hình vuông bị cắt đi là x (cm). Vậy chiều cao của hình hộp chữ nhật là x (cm),
Chiều dài tấm bìa sau khi cắt hay chiều dài hình hộp chữ nhật là: \(30 - 2x\) (cm).
Chiều rộng tấm bìa sau khi cắt hay chiều rộng hình hộp chữ nhật là: \(20 - 2x\)(cm).
Thể tích hình hộp chữ nhật là:
\(\begin{array}{l}(30 - 2x).(20 - 2x).x \\= (30 - 2x)(20x - 2{x^2})\\ = 30(20x - 2{x^2}) - 2x(20x - 2{x^2})\\ = 600x - 60{x^2} - 40{x^2} + 4{x^3}\\ = 4{x^3} - 100{x^2} + 600x (cm^3)\end{array}\)
Vậy đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi là \(4{x^3} - 100{x^2} + 600x\).
