I. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)
HĐ 2
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A’} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
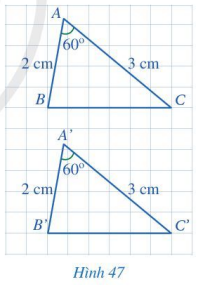

Đếm số ô vuông rồi so sánh BC và B’C’. Từ đó so sánh hai tam giác ABC và A’B’C’.

BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
LT -VD 1
Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.

Chứng minh tam giác OMQ bằng tam giác OPN. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Advertisements (Quảng cáo)

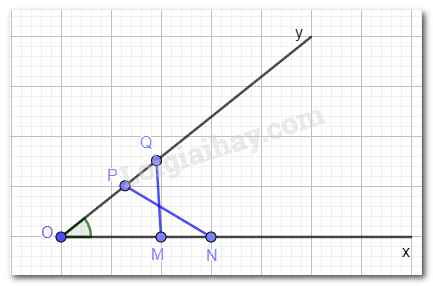
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.
Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)
\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)
LT - VD 2
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.

Muốn chứng minh MP = NP, ta chứng minh tam giác MOP bằng tam giác NOP.

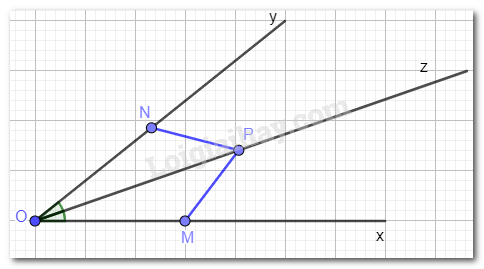
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)
