Giải bài 9.22 trang 76 SGK Toán lớp 7 tập 2 Kết nối tri thức với cuộc sống - Bài 34: Sự đồng quy của ba đường trung tuyến - ba đường phân giác trong một tam giác
![]()
Cho góc xOy khác góc bẹt. Dùng compa dựng đường tròn tâm O cắt Ox tại A và cắt Oy tại B. Sau đó dựng hai đường tròn tâm A, tâm B có bán kính bằng nhau sao cho chúng cắt nhau tại M nằm nên trong góc xOy. Chứng minh rằng tia OM là tia phân giác của góc xOy.
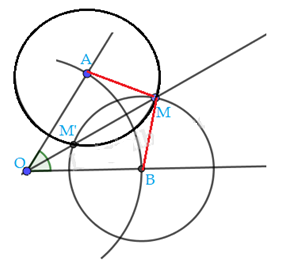
Ta có: AM = bán kính đường tròn tâm A
BM = bán kính đường tròn tâm B
Mà 2 đường tròn này có bán kính bằng nhau
Do đó, AM = BM
Xét \(\Delta \)OAM và \(\Delta \)ONM có:
OA = OB( = bán kính đường tròn tâm O)
Advertisements (Quảng cáo)
MA = MB
OM chung
\( \Rightarrow \) \(\Delta \)OAM và \(\Delta \)ONM ( c.c.c)
\( \Rightarrow \) \(\widehat {AOM} = \widehat {BOM}\) ( 2 góc tương ứng)
Mà OM nằm giữa 2 tia OA và OB
\( \Rightarrow \) OM là tia phân giác của góc AOB.
