![]()
Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC biết góc BAC bằng 120o.
![]()
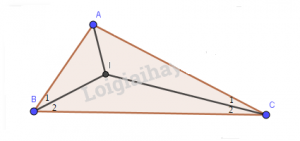
Vì BI là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CI là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Advertisements (Quảng cáo)
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat {BAC} = 180^\circ - 120^\circ = 60^\circ \\ \Rightarrow \widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}.\left( {\widehat {ABC} + \widehat {ACB}} \right) = \dfrac{1}{2}.60^\circ = 30^\circ \end{array}\)
Áp dụng định lí tổng ba góc trong tam giác BIC, ta có:
\(\begin{array}{l}\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ \\ \Rightarrow \widehat {BIC} = 180^\circ - \left( {\widehat {{B_2}} + \widehat {{C_2}}} \right) = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {BIC} = 150^\circ \)
