Bài 20. Cho góc \(xOy\) (h.73), Vẽ cung tròn tâm \(O\), cung tròn này cắt \(Ox, Oy\) theo thứ tự ở \(A,B\) (1). Vẽ các cung tròn tâm \(A\) và tâm \(B\) có cùng bán kính sao cho chúng cắt nhau ở điểm \(C\) nằm trong góc \(xOy\) ((2) (3)). Nối \(O\) với \(C\) (4). Chứng minh \(OC\) là tia phân giác của góc \(xOy\).
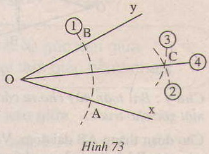

Vẽ cung tròn tâm \(O\), cung tròn này cắt \(Ox, Oy\) theo thứ tự ở \(A,B\) do đó \(OA=OB\) vì cùng bằng bán kính của cung tròn
Cung tròn tâm \(A\) và tâm \(B\) có cùng bán kính nên ta gọi bán kính là \(r\)
\(C\) là giao của hai cung tròn do đó \(C\) thuộc cung tròn tâm \(A\) nên \(AC=r\), \(C\) thuộc cung tròn tâm \(B\) nên \(BC=r\)
Suy ra \(AC=BC\)
Nối \(BC, AC\).
Advertisements (Quảng cáo)
Xét \(∆OBC\) và \(∆OAC\) có:
+) \(OB=OA\)
+) \(BC=AC\)
+) \(OC\) cạnh chung
Suy ra \(∆OBC = ∆OAC(c.c.c)\)
Nên \(\widehat{BOC}=\widehat{AOC}\) (hai góc tương ứng)
Vậy \(OC\) là tia phân giác của góc \(xOy\).
