Bài 52. Xem hình 36, hãy điền vào chỗ trống(...) để chứng minh định lí: ” Hai góc đối đỉnh thì bằng nhau”.
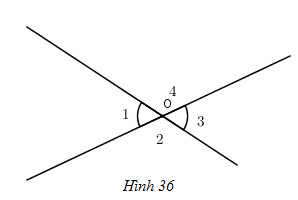
GT: ..
KL: ..
|
Các định lí |
Căn cứ khẳng định |
|
|
1 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) |
Vì … |
|
2 |
\(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) = ... |
Vì … |
|
3 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) |
Căn cứ vào … |
|
4 |
\(\widehat{O_{1}}\) = \(\widehat{O_{3}}\) |
Căn cứ vào … |
Tương tự chứng minh \(\widehat{O_{2}}\) = \(\widehat{O_{4}}\)

Giả thiết: \(\widehat{O_{1}}\) đối đỉnh \(\widehat{O_{3}}\).
Kết luận: \(\widehat{O_{1}}\) = \(\widehat{O_{3}}\)
|
Các định lí |
Căn cứ khẳng định |
|
|
1 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) |
Advertisements (Quảng cáo) Vì \(\widehat{O_{1}}\) và \(\widehat{O_{2}}\) kề bù |
|
2 |
\(\widehat{O_{3}}\) + \(\widehat{O_{2}}=180^0\) |
Vì \(\widehat{O_{2}}\) và \(\widehat{O_{2}}\) kề bù |
|
3 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) |
Căn cứ vào 1 và 2 |
|
4 |
\(\widehat{O_{1}}\) = \(\widehat{O_{3}}\) |
Căn cứ vào 3 |
Chứng minh \(\widehat{O_{2}}\) = \(\widehat{O_{4}}\)
|
Các định lí |
Căn cứ khẳng định |
|
|
1 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) |
Vì \(\widehat{O_{1}}\) và \(\widehat{O_{2}}\) kề bù |
|
2 |
\(\widehat{O_{1}}\) + \(\widehat{O_{4}}=180^0\) |
Vì \(\widehat{O_{1}}\) và \(\widehat{O_{4}}\) kề bù |
|
3 |
\(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{1}}\) + \(\widehat{O_{4}}\) |
Căn cứ vào 1 và 2 |
|
4 |
\(\widehat{O_{2}}\) = \(\widehat{O_{4}}\) |
Căn cứ vào 3 |
