Bài 59. Hình 41 cho biết \(d // d’ // d’’\) và hai góc \(60^0 ,110^0\). Tính các góc
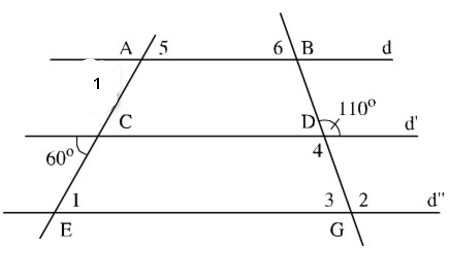

Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì \(d’ //d’’\) có: \(\widehat {{E_1}}\) và góc \(60^0\) là hai góc so le trong nên \(\widehat {{E_1}} = 60^0\)
+Vì \(d’ // d’’\) có: \(\widehat {{G_2}}\) và góc \(110^0\) là hai góc đồng vị nên \(\widehat {{G_2}} = 110^0\)
+ \(\widehat {{G_2}} + {\widehat G_3} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {{G_3}} = {180^0} - \widehat {{G_2}} = {180^0} - {110^0} = {70^0}\)
Advertisements (Quảng cáo)
+) \(\widehat {{D_4}} = 110^0\) (vì là hai góc đối đỉnh)
+) \(\widehat {{A_5}}\) = \(\widehat {{A_1}}\) (Hai góc đối đỉnh)
Mà \(\widehat {{A_1}} = 60^0\) (vì là hai góc đồng vị)
Nên \(\widehat {{A_5}} = 60^0\) .
+ \(\widehat {{B_6}}\) = \(\widehat {{B_2}}\) (vì là hai góc đối đỉnh)
Mà \(\widehat {{B_2}}\) + \(110^0\) = \(180^0\) (hai góc trong cùng phía)
Nên \(\widehat {{B_2}}\) = \(180^0\) - \(110^0\) = \(70^0\).
Do đó: \(\widehat {{B_6}}\) = \(70^0\)
