Bài 65. Các tam giác ABC cân tại A. Bài 65 trang 137 – Sách giáo khoa toán 7 tập 1 – Các trường hợp bằng nhau của tam giác vuông
Advertisements (Quảng cáo)
Bài 65. Các tam giác ABC cân tại A(\(\widehat{A}\)<900). Vẽ BH ⊥ A (H thuộc AC), CK⊥ AB (K thuộc AB)
a) Chứng minh rằng AH=AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của góc A.
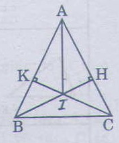
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
Advertisements (Quảng cáo)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra \(\widehat{IAK}\)=\(\widehat{IAH}\)
Vậy AI là tia phân giác của góc A.
Mục lục môn Toán 8
- Tam giác cân
- Định lí Pytago
- Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương II: Tam giác
- Thu thập số liệu thống kê, tần số.
TOÁN 7 TẬP 2 - ĐẠI SỐ
Chương 3. Thống kê