Cho tam giác \(ABC\) cân tại \(A,AB=10\)cm, \(BC=12\)cm. Gọi \(I\) là giao điểm của các đường phân giác của tam giác \(ABC\). Tính độ dài \(AI\).
Tam giác \(A’B’C’\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}\) ; \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}\).
Kí hiệu là \(\Delta A’B’C’\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k\) gọi là tỉ số đồng dạng.
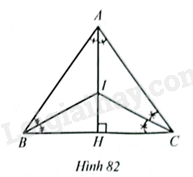
Gọi \(H\) là giao điểm của hai đường thẳng \(AI\) và \(BC\). Do tam giác \(ABC\) cân tại \(A\) nên đường phân giác \(AI\) cũng là đường cao, đường trung tuyến. Do đó \(BH=\frac{BC}{2}=6\)cm. Tam giác \(AHB\) vuông tại \(H\) nên \(A{{H}^{2}}=A{{B}^{2}}-B{{H}^{2}}={{10}^{2}}-{{6}^{2}}=64\), suy ra \(AH=8\)cm. Ta có \(\frac{AI}{IH}=\frac{AB}{BH}\) suy ra \(\frac{AI}{AI+IH}=\frac{AB}{AB+BH}\) hay \(\frac{AI}{8}=\frac{10}{10+6}=\frac{5}{8}\). Vậy \(AI=5\)cm.