
Cho hình bình hành \(ABCD\left( AC>BD \right)\). Vẽ \(CE\) vuông góc với đường thẳng \(AB\) tại \(E,CF\) vuông góc với đường thẳng \(AD\) tại \(F,BH\) vuông góc với đường thẳng \(AC\) tại \(H\). Chứng minh:
a) \(\Delta ABH\backsim \Delta ACE;\Delta CBH\backsim \Delta ACF\)
b) \(B{{H}^{2}}=HK.HQ\), biết tia \(BH\) cắt đường thẳng \(CD\) tại \(Q\); cắt cạnh \(AD\) tại \(K\).

Tam giác \(A’B’C’\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}\) ; \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}\).
Kí hiệu là \(\Delta A’B’C’\backsim \Delta ABC\).
Advertisements (Quảng cáo)
Tỉ số các cạnh tương ứng \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k\) gọi là tỉ số đồng dạng.

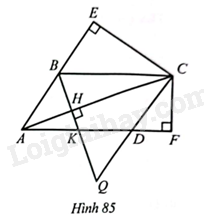
a) Ta có hai tam giác \(ABH\) và \(ACE\) đều là các tam giác vuông và \(\widehat{BAH}=\widehat{EAC}\). Suy ra \(\Delta ABH\backsim \Delta ACE\). Hai tam giác \(CBH\) và \(ACF\) đều là các tam giác vuông và \(\widehat{BCH}=\widehat{CAF}\) , suy ra \(\Delta CBH\backsim \Delta ACF\).
b) Do \(AB//CQ\) nên \(\frac{QH}{BH}=\frac{CH}{AH}\)
Lại có \(BC//AK\) nên \(\frac{BH}{HK}=\frac{CH}{AH}\)
Suy ra \(\frac{QH}{BH}=\frac{BH}{HK}\). Hay \(B{{H}^{2}}=HK.HQ\).
