
Cho hình thang \(ABCD\), \(AB//CD\), \(\widehat{DAB}=\widehat{DBC},\frac{AB}{BD}=\frac{2}{5}\). Tính diện tích tam giác \(BDC\), biết diện tích tam giác \(ABD\) là \(44,8c{{m}^{2}}\).

Tam giác \(A’B’C’\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}\) ; \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}\).
Kí hiệu là \(\Delta A’B’C’\backsim \Delta ABC\).
Advertisements (Quảng cáo)
Tỉ số các cạnh tương ứng \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k\) gọi là tỉ số đồng dạng.

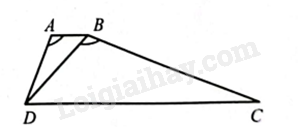
Có \(\Delta ABD\backsim \Delta BDC\) do \(\widehat{DAB}=\widehat{DBC}\); \(\widehat{ABD}=\widehat{BDC}\). Do đó, tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(BDC\) bằng bình phương của tỉ số đồng dạng.
Suy ra diện tích tam giác \(ABD\) (kí hiệu là \({{S}_{\Delta ABD}}\)) bằng \(\frac{4}{25}\) diện tích tam giác \(BDC\) (kí hiệu là \({{S}_{\Delta BDC}}\)) hay \({{S}_{\Delta ABD}}=\frac{4}{25}.{{S}_{\Delta BDC}}\).
Do đó: \(44,8=\frac{4}{25}.{{S}_{\Delta BDC}}\) hay \({{S}_{\Delta BCD}}=44,8:\frac{4}{25}=11,2.25=280\left( c{{m}^{2}} \right)\).
