
Cho tam giác \(ABC\) có ba góc nhọn, các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Chứng minh:
a) \(\Delta EBH\backsim \Delta DCH,\Delta ADE\backsim \Delta ABC\);
b) \(DB\) là tia phân giác của góc \(EDI\), với \(I\) là giao điểm của \(AH\) và \(BC\).

Tam giác \(A’B’C’\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}\) ; \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}\).
Advertisements (Quảng cáo)
Kí hiệu là \(\Delta A’B’C’\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k\) gọi là tỉ số đồng dạng.

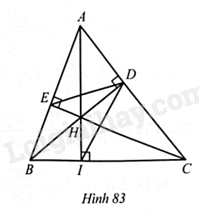
a) Vì các tam giác \(EBH\) và \(DCH\) đều là các tam giác vuông và \(\widehat{EBH}=\widehat{DHC}\) (hai góc đối đỉnh) nên \(\Delta EBH\backsim \Delta DCH\). Tương tự, ta có các tam giác \(ABH\) và \(ACE\) là các tam giác vuông và \(\widehat{BAD}=\widehat{CAE}\) nên \(\Delta ABH\backsim \Delta ACE\). Suy ra \(\frac{AB}{AC}=\frac{AD}{AE}\) hay \(\frac{AB}{AD}=\frac{AC}{AE}\). Mà \(\widehat{BAC}=\widehat{DAE}\) suy ra \(\Delta ADE\backsim \Delta ABC\).
b) Do \(\Delta ADE\backsim \Delta ABC\) nên \(\widehat{ADE}=\widehat{CBA}\) (1). Tương tự cách chứng minh ở câu a, ta có \(\Delta CDI\backsim \Delta CBA\) (2). Từ (1) và (2), ta có \(\widehat{ADE}=\widehat{CDI}\).
Do đó \(90{}^\circ -\widehat{ADE}=90{}^\circ -\widehat{CDI}\) hay \(\widehat{EDB}=\widehat{BDI}\). Vậy \(DB\) là đường phân giác của góc \(EDI\).
