
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Chứng minh tứ giác ANCQ là hình bình hành.

a) Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
b) Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.

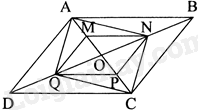
a) Vì ABCD là hình bình hành nên \(AO = CO,BO = DO\), \(AB = CD,AD = BC\), AB//CD, AD//BC
Vì M, P lần lượt là trung điểm của AO, CO nên \(MA = MO = \frac{1}{2}AO = \frac{1}{2}CO = OP = PC\)
Advertisements (Quảng cáo)
Vì N, Q lần lượt là trung điểm của BO, DO nên \(NB = NO = \frac{1}{2}BO = \frac{1}{2}DO = OQ = QD\)
Tứ giác MNPQ có: \(MO = OP,NO = OQ\) nên tứ giác MNPQ là hình bình hành.
b) Vì AB//CD nên \(\widehat {ABN} = \widehat {QDC}\) (hai góc so le trong)
Tam giác ABN và tam giác CDQ có:
\(AB = CD\left( {cmt} \right),\widehat {ABN} = \widehat {QDC}\left( {cmt} \right),NB = DQ\left( {cmt} \right)\)
Do đó, \(\Delta ABN = \Delta CDQ\left( {c - g - c} \right)\) nên \(AN = CQ\)
Vì AD//CB nên \(\widehat {QDA} = \widehat {NBC}\) (hai góc so le trong)
Tam giác ADQ và tam giác CBN có:
\(AD = CB\left( {cmt} \right),\widehat {QDA} = \widehat {NBC}\left( {cmt} \right),DQ = NB\left( {cmt} \right)\)
Do đó, \(\Delta ADQ = \Delta CBN\left( {c - g - c} \right)\) nên \(AQ = CN\)
Tứ giác ANCQ có: \(AN = CQ\), \(AQ = CN\) nên tứ giác ANCQ là hình bình hành.
