
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc \(\widehat {ADB},\widehat {DBC}\left( {E \in AB,K \in CD} \right)\)
a) Chứng minh DE//BK.
b) Giả sử \(DE \bot AB\). Chứng minh \(DA = DB\).
c) Trong trường hợp \(DE \bot AB\), tìm số đo của \(\widehat {ADB}\) để tứ giác DEBK là hình vuông.

Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc \(\widehat {ADB},\widehat {DBC}\left( {E \in AB,K \in CD} \right)\)
a) Chứng minh DE//BK.
b) Giả sử \(DE \bot AB\). Chứng minh \(DA = DB\).
c) Trong trường hợp \(DE \bot AB\), tìm số đo của \(\widehat {ADB}\) để tứ giác DEBK là hình vuông.
Advertisements (Quảng cáo)

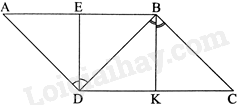
a) Vì ABCD là hình bình hành nên AD//BC. Suy ra \(\widehat {ADB} = \widehat {DBC}\) (hai góc so le trong)
Do đó: \(\frac{{\widehat {ADB}}}{2} = \frac{{\widehat {DBC}}}{2}\), suy ra \(\widehat {EDB} = \widehat {KBD}\)
Mà hai góc này ở vị trí so le trong nên DE//BK.
b) Tam giác DAB có DE vừa là đường cao đồng thời là phân giác nên tam giác DAB cân tại D. Do đó, \(DA = DB\)
c) Tứ giác DEBK có: DE//BK, EB//DK nên tứ giác DEBK là hình bình hành. Mà \(\widehat {DEB} = {90^0}\) nên DEBK là hình chữ nhật.
Để hình chữ nhật DEBK là hình vuông thì \(DE = EB\)
Mà tam giác DAB cân tại D nên DE là trung tuyến của tam giác DAB.
Suy ra: \(DE = EB = AE = \frac{{AB}}{2}\), do đó tam giác DAB vuông tại D hay \(\widehat {ADB} = {90^0}\)
