Sử dụng kiến thức về định nghĩa hai tam giác đồng dạng để tính. Hướng dẫn cách giải/trả lời bài 3 trang 59 sách bài tập (SBT) toán 8 - Chân trời sáng tạo tập 2 - Bài 1. Hai tam giác đồng dạng. Trong Hình 6, cho biết $\Delta ABC\backsim \Delta DEF$ Tính số đo góc E....
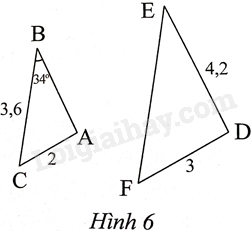
Trong Hình 6, cho biết $\Delta ABC\backsim \Delta DEF$
a) Tính số đo góc E.
b) Tính độ dài các đoạn thẳng AB và EF.
Advertisements (Quảng cáo)
Sử dụng kiến thức về định nghĩa hai tam giác đồng dạng để tính: Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu \(\widehat {A’} = \widehat A,\widehat {B’} = \widehat B,\widehat {C’} = \widehat C,\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}} = k\) (k gọi là tỉ số đồng dạng)
a) Vì $\Delta ABC\backsim \Delta DEF$ nên $\widehat{E}=\widehat{B}={{34}^{0}}$
b) Vì $\Delta ABC\backsim \Delta DEF$ nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\), hay \(\frac{{AB}}{{4,2}} = \frac{{3,6}}{{EF}} = \frac{2}{3}\)
Do đó, \(AB = \frac{2}{3}.4,2 = 2,8;EF = \frac{{3,6.3}}{2} = 5,4\)