
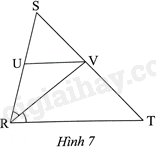
Trong Hình 7, cho biết RV là tia phân giác của góc SRT và UV//RT. Chứng minh rằng:
a) $\Delta SUV\backsim \Delta SRT$.
b) \(\frac{{SU}}{{UR}} = \frac{{SR}}{{RT}}\).

Sử dụng kiến thức về định lí về hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Advertisements (Quảng cáo)

a) Tam giác SRT có: UV//RT nên $\Delta SUV\backsim \Delta SRT$
b) Vì UV//RT nên \(\widehat {RVU} = \widehat {VRT}\) (hai góc so le trong)
Mà \(\widehat {URV} = \widehat {VRT}\) (vì RV là tia phân giác của góc SRT) nên \(\widehat {RVU} = \widehat {URV}\)
Do đó, tam giác RUV cân tại U. Suy ra \(UR = UV\).
Lại có: $\Delta SUV\backsim \Delta SRT$ nên \(\frac{{SU}}{{SR}} = \frac{{UV}}{{RT}}\). Do đó, \(\frac{{SU}}{{UR}} = \frac{{SR}}{{RT}}\)
