Bài 3 trang 68 SBT Toán 8 - Chân trời sáng tạo tập 2: Quan sát Hình 7, biết tứ giác ABHD là hình chữ nhật. Chứng minh rằng: $B{{D}^{2}}=AB. DC$. $A{{D}^{2}}=BM. BC$...

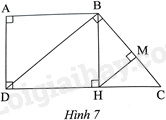
Quan sát Hình 7, biết tứ giác ABHD là hình chữ nhật. Chứng minh rằng:

a) $B{{D}^{2}}=AB.DC$.

b) $A{{D}^{2}}=BM.BC$.

Sử dụng kiến thức về áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông: Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

a) Vì ABHD là hình chữ nhật nên AB//DH, do đó $\widehat{ABD}=\widehat{BDH}$ (hai góc so le trong)

Tam giác ABD và tam giác BDC có: $\widehat{A}=\widehat{DBC}={{90}^{0}},\widehat{ABD}=\widehat{BDH}\left( cmt \right)$

Do đó, $\Delta ABD\backsim \Delta BDC\left( g.g \right)$, do đó $\frac{AB}{BD}=\frac{BD}{DC}$. Vậy $B{{D}^{2}}=AB.DC$

b) Tam giác BMH và tam giác BHC có: $\widehat{HMB}=\widehat{BHC}={{90}^{0}},\widehat{HBM}\ chung$

Do đó, $\Delta BHM\backsim \Delta BCH\left( g.g \right)$, do đó $\frac{BM}{BH}=\frac{BH}{BC}$, hay $B{{H}^{2}}=BM.BC$

Vì ABHD là hình chữ nhật nên $AD=BH$. Do đó, $A{{D}^{2}}=BM.BC$