
Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và tia phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN//AD.

Sử dụng kiến thức về tính chất của đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.

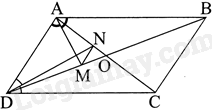
Gọi O là giao điểm của AC và BD nên \(AC = 2AO,BD = 2DO\)
Advertisements (Quảng cáo)
Vì DN là phân giác của góc ADC trong tam giác ADC nên: \(\frac{{NA}}{{NC}} = \frac{{AD}}{{DC}}\)
Vì AM là phân giác của góc DAB trong tam giác ADB nên: \(\frac{{MD}}{{MB}} = \frac{{AD}}{{AB}} = \frac{{AD}}{{DC}}\)
Do đó, \(\frac{{NA}}{{NC}} = \frac{{MD}}{{MB}}\)
Suy ra: \(\frac{{NA}}{{MD}} = \frac{{NC}}{{MB}} = \frac{{NA + NC}}{{MD + MB}} = \frac{{AC}}{{BD}} = \frac{{AO}}{{DO}}\)
Do đó, \(\frac{{AN}}{{AO}} = \frac{{MD}}{{DO}}\)
Tam giác ADO có: \(\frac{{AN}}{{AO}} = \frac{{MD}}{{DO}}\) nên MN//AD (định lí Thalès đảo).
