
Cho tam giác ABC, điểm I nằm trong tam giác. Lấy điểm D trên IA, qua D kẻ đường thẳng song song với AB, cắt IB tại E. Qua E kẻ đường thẳng song song với BC, cắt IC tại F. Chứng minh rằng: DF//AC

+ Sử dụng kiến thức về định lí Thalès để chứng minh \(\frac{{ID}}{{IA}} = \frac{{IF}}{{IC}}\): Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ. + Sử dụng kiến thức về định lí Thalès đảo để chứng minh DF//AC: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Advertisements (Quảng cáo)
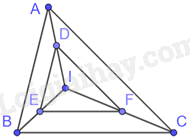
Tam giác AIB có DE//AB (gt) nên theo định lí Thalès ta có: \(\frac{{ID}}{{IA}} = \frac{{IE}}{{IB}}\)
Tam giác CIB có FE//CB (gt) nên theo định lí Thalès ta có: \(\frac{{IF}}{{IC}} = \frac{{IE}}{{IB}}\)
Do đó, \(\frac{{ID}}{{IA}} = \frac{{IF}}{{IC}}\)
Tam giác AIC có: \(\frac{{ID}}{{IA}} = \frac{{IF}}{{IC}}\) nên DF//AC (định lí Thalès đảo)
