
Cho hình bình hành ABCD, AC cắt BD tại O. Đường phân giác góc A cắt BD tại M, đường phân giác góc D cắt AC tại N. Chứng minh MN//AD.

+ Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh \(\frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}\): Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
+ Sử dụng kiến thức về định lí Thalès đảo để chứng minh MN//AD: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

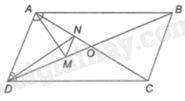
Vì AM là phân giác của góc BAD trong tam giác ABD nên \(\frac{{AB}}{{AD}} = \frac{{MB}}{{MD}}\) (tính chất đường phân giác trong tam giác)
Advertisements (Quảng cáo)
Vì DN là phân giác của góc ADC trong tam giác ACD nên \(\frac{{DC}}{{AD}} = \frac{{NC}}{{NA}}\) (tính chất đường phân giác trong tam giác)
Vì tứ giác ABCD là hình bình hành nên \(AB = CD\)
Do đó, \(\frac{{MB}}{{MD}} = \frac{{NC}}{{NA}}\), suy ra \(\frac{{MB}}{{MD}} + 1 = \frac{{NC}}{{NA}} + 1\)
Hay \(\frac{{MB + MD}}{{MD}} = \frac{{NC + NA}}{{NA}}\), do đó \(\frac{{BD}}{{MD}} = \frac{{AC}}{{NA}}\)
Vì ABCD là hình bình hành nên \(BD = 2DO,AC = 2AO\)
Do đó, \(\frac{{2DO}}{{DM}} = \frac{{2AO}}{{AN}}\) hay \(\frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}\)
Tam giác DAO có: \(\frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}\) nên MN//AD (định lí Thalès đảo)
