Câu 1
Cho tam giác ABC có \(BC = 13cm.\) E và F lần lượt là trung điểm của AB, AC. Độ dài EF bằng:
A. 13cm
B. 26cm
C. 6,5cm
D. 3cm

Sử dụng kiến thức về đường trung bình của tam giác để tìm EF: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

Tam giác ABC có E và F lần lượt là trung điểm của AB, AC nên EF là đường trung bình của tam giác. Do đó, \(FE = \frac{1}{2}BC = 6,5cm\)
Chọn C
Câu 2
Độ dài x trong Hình 5.13 là
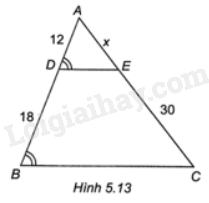
A. 20
B. 50
C. 12
D. 30

Sử dụng kiến thức về định lí Thalès để tính x: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ

Vì \(\widehat {ADE} = \widehat B\) (gt), mà hai góc này ở vị trí đồng vị nên DE//BC.
Tam giác ABC có DE//BC nên theo định lí Thalès ta có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)
\(\frac{{12}}{{18}} = \frac{x}{{30}}\) nên \(x = \frac{{12.30}}{{18}} = 20\)
Chọn A
Câu 3
Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC. Khẳng định nào đúng?
A. \(MN = \frac{1}{2}AC\)
B. \(BC = \frac{1}{2}IK\)
C. \(MN > IK\)
D. \(MN = IK\)

Sử dụng kiến thức về đường trung bình của tam giác để tìm câu đúng: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

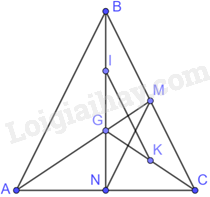
Tam giác ABC cân tại B nên \(AB = BC\) (1)
Tam giác ABC có M, N lần lượt là trung điểm của BC, AC nên MN là đường trung bình của tam giác. Do đó, \(MN = \frac{1}{2}AB\) (2)
Tam giác GBC có I, K lần lượt là trung điểm của BG, GC nên IK là đường trung bình của tam giác. Do đó, \(IK = \frac{1}{2}BC\) (3)
Từ (1), (2) và (3) suy ra: \(MN = IK\)
Chọn D.
Câu 4
Cho hình thang ABCD (AB//DC). Gọi O là giao điểm của AC và BD. Xét các khẳng định sau:
(1) \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\)
(2) \(OA.OD = OB.OC\)
(3) \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3

Sử dụng kiến thức về định lí Thalès để tìm khẳng định đúng: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

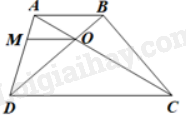
Qua O kẻ OM//AB//CD (M thuộc AD).
Tam giác ADC có: OM//DC nên \(\frac{{OA}}{{OC}} = \frac{{MA}}{{MD}},\frac{{OA}}{{AC}} = \frac{{AM}}{{AD}}\)
Tam giác ADB có: OM//AB nên \(\frac{{OB}}{{OD}} = \frac{{MA}}{{MD}},\frac{{BO}}{{BD}} = \frac{{AM}}{{AD}}\)
Do đó, \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\) và \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Vì \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\) nên \(OA.OD = OB.OC\)
Vậy khẳng định (3) và (2) đúng.
Chọn C.
Câu 5
Cho Hình 5.14, biết DE//AC. Độ dài x là
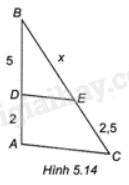
A. 5
B. 7
C. 6,5
D. 6,25

Sử dụng kiến thức về định lí Thalès để tính x: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Tam giác ABC có: DE//AC nên theo định lí Thalès ta có: \(\frac{{DB}}{{DA}} = \frac{{BE}}{{EC}}\)
\(\frac{5}{2} = \frac{x}{{2,5}}\) nên \(x = \frac{{5.2,5}}{2} = 6,25\)
Chọn D
Câu 6
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Biết \(AG = 4cm\), độ dài của EI, DK là
A. \(EI = DK = 3cm\)
B. \(EI = 3cm,DK = 2cm\)
C. \(EI = DK = 2cm\)
D. \(EI = 1cm,DK = 2cm\)

Sử dụng kiến thức về đường trung bình của tam giác để tìm EI, DK: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy

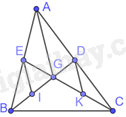
Vì BD, CE là các đường trung tuyến của tam giác ABC nên D, E lần lượt là trung điểm của AC, AB.
Tam giác ABG có I, E lần lượt là trung điểm của GB, AB nên IE là đường trung bình của tam giác ABG. Do đó, \(EI = \frac{1}{2}AG = 2cm\)
Tam giác AGC có D, K lần lượt là trung điểm của AC, GC nên DK là đường trung bình của tam giác AGC. Do đó, \(DK = \frac{1}{2}AG = 2cm\)
Chọn C.
Câu 7
Advertisements (Quảng cáo)
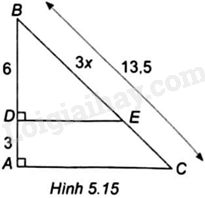
Cho Hình 5.15, biết \(ED \bot AB,AC \bot AB.\) Khi đó, x có giá trị là
A. 2,5
B. 2
C. 3
D. 4

Sử dụng kiến thức về định lí Thalès để tính x: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Vì \(ED \bot AB,AC \bot AB\) nên ED//AC
Tam giác ABC có: ED//AC nên theo theo định lí Thalès ta có: \(\frac{{BD}}{{AB}} = \frac{{BE}}{{BC}}\)
\(\frac{6}{{3 + 6}} = \frac{{3x}}{{13,5}}\) nên \(3x = \frac{{6.13,5}}{9} = 9\), suy ra \(x = \frac{9}{3} = 3\)
Chọn C
Câu 8
Cho \(\Delta ABC\). Tia phân giác góc trong của góc A cắt BC tại D. Cho \(AB = 6,AC = x,BD = 9,BC = 21\). Độ dài x bằng
A. 4
B. 6
C. 12
D. 14

Sử dụng kiến thức về tính chất đường phân giác của tam giác để tìm x: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

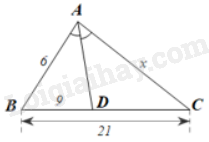
Vì AD là tia phân giác góc BAC của tam giác ABC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
\(\frac{9}{{21 - 9}} = \frac{6}{x}\), suy ra \(x = \frac{{12.6}}{9} = 8\)
Không có đáp án
Câu 9
Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết \(AB = 3cm,BD = 4cm,CD = 6cm\). Độ dài AC bằng
A. 4cm
B. 5cm
C. 6cm
D. 4,5cm

Sử dụng kiến thức về tính chất đường phân giác của tam giác để tìm AC: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

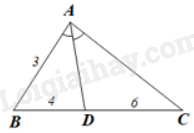
Vì AD là tia phân giác góc BAC của tam giác ABC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
\(\frac{4}{6} = \frac{3}{x}\), suy ra \(x = \frac{{6.3}}{4} = 4,5\left( {cm} \right)\)
Chọn D
Câu 10
Cho \(\Delta ABC\) đều, cạnh 3cm; M, N lần lượt là trung điểm AB, AC. Chu vi của tứ giác MNCB bằng
A. 8cm
B. 7,5cm
C. 6cm
D. 7cm

Sử dụng kiến thức về đường trung bình của tam giác để tính: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.

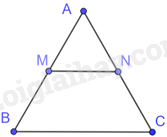
Tam giác ABC đều \(AB = AC = BC = 3cm\)
Vì M, N lần lượt là trung điểm AB, AC nên \(BM = \frac{1}{2}AB = \frac{3}{2}cm,NC = \frac{1}{2}AC = \frac{3}{2}cm\)
Tam giác ABC có M, N lần lượt là trung điểm AB, AC nên MN là đường trung bình của tam giác ABC.
Suy ra \(MN = \frac{1}{2}BC = \frac{3}{2}cm\)
Chu vi tứ giác MNCB là:
\(BM + MN + NC + BC = \frac{3}{2} + \frac{3}{2} + \frac{3}{2} + 3 = 7,5\left( {cm} \right)\)
Chọn B
Câu 11
Cho tam giác ABC có \(AB = 6cm,AC = 8cm,BC = 10cm.\) Gọi H, I, K lần lượt là trung điểm của AB, BC, AC. Chu vi tứ giác AHIK bằng:
A. 7cm
B. 14cm
C. 24cm
D. 12cm

Sử dụng kiến thức về đường trung bình của tam giác để tính: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy

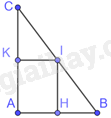
Vì K, H lần lượt là trung điểm của AB, AC nên \(AK = \frac{1}{2}AC = 4cm,AH = \frac{1}{2}AB = 3cm\)
Tam giác ABC có H, I lần lượt là trung điểm của AB, BC nên HI là đường trung bình của tam giác ABC nên \(HI = \frac{1}{2}AC = 4cm\)
Tam giác ABC có K, I lần lượt là trung điểm của AC, BC nên KI là đường trung bình của tam giác ABC nên \(KI = \frac{1}{2}AB = 3cm\)
Chu vi tứ giác AHIK là:
\(KI + HI + AH + AK = 3 + 4 + 3 + 4 = 14\left( {cm} \right)\)
Chọn B.
Câu 12
Cho hình thoi ABCD có M là trung điểm của AD, đường chéo AC cắt BM tại điểm E (H.5.16)
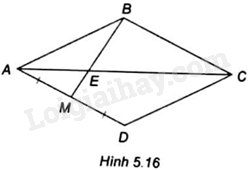
Tỉ số \(\frac{{EM}}{{EB}}\) bằng
A. \(\frac{1}{3}\)
B. 2
C. \(\frac{1}{2}\)
D. \(\frac{2}{3}\)

Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

Vì tứ giác ABCD là hình thoi nên AC là tia phân giác của góc BAD và \(AD = AB\)
Tam giác ABM có AE là tia phân giác của góc BAM nên \(\frac{{EM}}{{EB}} = \frac{{AM}}{{AB}}\) (tính chất đường phân giác trong tam giác).
Mà M là trung điểm của AD nên \(AM = \frac{1}{2}AD = \frac{1}{2}AB\)
Do đó, \(\frac{{EM}}{{EB}} = \frac{{\frac{1}{2}AB}}{{AB}} = \frac{1}{2}\)
Chọn C
