
Anh Nam đang tiết kiệm tiền để mua một chiếc máy tính mới với giá 15 triệu đồng. Anh Nam đã có 4,5 triệu đồng và dự định sẽ tiết kiệm 300 nghìn đồng mỗi tuần.
a) Viết hàm số \(y = f\left( x \right)\) biểu thị số tiền y (triệu đồng) mà anh Nam đã tiết kiệm được sau x (tuần).
b) Vẽ đồ thị của hàm số tìm được ở câu a. Từ đó xác định số tuần anh Nam sẽ tiết kiệm đủ tiền để mua chiếc máy tính đó.

* Sử dụng khái niệm hàm số bậc nhất để viết hàm số: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)
* Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ các đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
Advertisements (Quảng cáo)
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)

a) Hàm số \(y = f\left( x \right)\) biểu thị số tiền y (triệu đồng) mà anh Nam đã tiết kiệm được sau x (tuần) là: \(y = f\left( x \right) = 4,5 + 0,3x\) (triệu đồng)
b) Đồ thị hàm số \(y = f\left( x \right) = 4,5 + 0,3x\) đi qua hai điểm \(A\left( {0;4,5} \right);B\left( { - 15;0} \right)\)
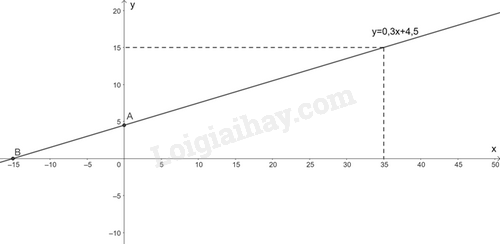
Từ đồ thị ta thấy, để mua được máy tính giá 15 triệu đồng thì anh Nam tiết kiệm trong 35 tuần.
