Tìm giá trị nguyên của n để giá trị của biểu thức \(3{n^3} + 10{n^2} - 5\) chia hết cho giá trị của biểu thức 3n+1

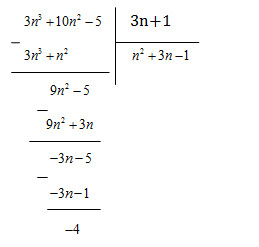
\( \Rightarrow 3{n^3} + 10{n^2} - 5 = \left( {3n + 1} \right)\left( {{n^2} + 3n - 1} \right) - 4\)
Để phép chia đó là phép chia hết thì \(4 \vdots 3n + 1 \Rightarrow 3n + 1 \in \) Ư(4)
\(3n + 1 \in \left\{ { - 4; - 2; - 1;1;2;4} \right\}\)
\(3n + 1 = - 4 \Rightarrow 3n = - 5 \Rightarrow n = \notin Z:\)loại
Advertisements (Quảng cáo)
\(3n + 1 = - 2 \Rightarrow 3n = - 3 \Rightarrow n = - 1\)
\(3n + 1 = - 1 \Rightarrow 3n = - 2 \Rightarrow n \notin Z\): loại
\(3n + 1 = 1 \Rightarrow 3n = 0 \Rightarrow n = 0\)
\(3n + 1 = 2 \Rightarrow 3n = 1 \Rightarrow n \notin Z\): loại
\(3n + 1 = 4 \Rightarrow 3n = 3 \Rightarrow n = 1\)
Vậy \(n \in \left\{ { - 1;0;1} \right\}\) thì \(3{n^3} + 10{n^2} - 5\) chia hết cho 3n+1
