Trả lời bài 1 trang 85 SGK Toán 8 – Cánh diều Bài 8. Trường hợp đồng dạng thứ ba của tam giác. Cho Hình 86. Chứng minh \(\Delta MNP \backsim \Delta ABC\) Tìm \(x\).
Cho Hình 86.
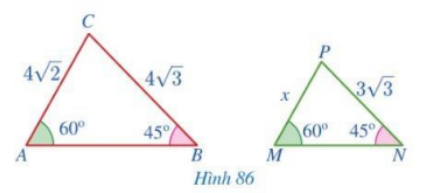
a) Chứng minh \(\Delta MNP \backsim \Delta ABC\)
b) Tìm \(x\).
a) Chứng minh \(\Delta MNP \backsim \Delta ABC\) theo trường hợp đồng dạng thứ ba.
Advertisements (Quảng cáo)
b) Từ hai tam giác đồng dạng, suy ra tỉ số đồng dạng tương ứng rồi tìm \(x\).
a) Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat A = \widehat M = 60^\circ \\\widehat B = \widehat N = 45^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g)
b) Vì \(\Delta MNP \backsim \Delta ABC\) nên \(\frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (Tỉ số đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{4\sqrt 2 }}{x} = \frac{{4\sqrt 3 }}{{3\sqrt 3 }}\\ \Rightarrow x = \frac{{4\sqrt 2 .3\sqrt 3 }}{{4\sqrt 3 }} = 3\sqrt 2 \end{array}\)