Hoạt động1
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A’} = \widehat A,\,\,\widehat {B’} = \widehat B\) và \(A’B’ \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A’M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A’MN = \Delta ABC\). Từ đó suy ra \(\Delta A’B’C’ \backsim \Delta ABC\).
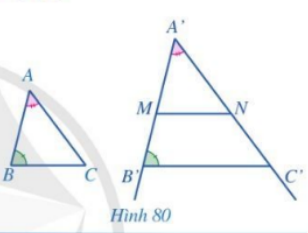

Chứng minh \(\Delta A’MN = \Delta ABC\) theo các trường hợp đã học từ đó chứng minh \(\Delta A’B’C’ \backsim \Delta ABC\).

Vì \(MN\parallel B’C’\) nên \(\widehat {A’MN} = \widehat {A’B’C’}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A’} = \widehat A;\,\,A’M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A’MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B’C’\) nên \(\Delta A’MN \backsim \Delta A’B’C’\)
Advertisements (Quảng cáo)
\( \Rightarrow \Delta ABC \backsim \Delta A’B’C’\)
Luyện tập1
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).

Tìm số đo các góc còn lại của hai tam giác rồi chứng minh \(\Delta ABC \backsim \Delta MNP\) theo trường hợp đồng dạng thứ ba.

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
