
Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:
a) \(\Delta ACD \backsim \Delta BCE\) và \(CA.CE = CB.CD\)
b) \(\Delta ACD \backsim \Delta AHE\) và \(AC.AE = AD.AH\)

Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba rồi suy ra hệ số đồng dạng tương ứng.

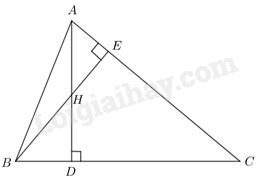
a) Xét tam giác ACD và tam giác BCE có:
Advertisements (Quảng cáo)
\(\widehat {ADC} = \widehat {BEC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ACD \backsim \Delta BCE\) (g-g)
\( \Rightarrow \frac{{CA}}{{CB}} = \frac{{CD}}{{CE}}\) (Tỉ số đồng dạng) \( \Rightarrow CA.CE = CB.CD\)
b) Xét tam giác ACD và tam giác AHE có:
\(\widehat {ADC} = \widehat {AEH} = 90^\circ ;\,\,\widehat A\) chung
\( \Rightarrow \Delta ACD \backsim \Delta AHE\) (g-g)
\( \Rightarrow \frac{{AC}}{{AH}} = \frac{{AD}}{{AE}}\) (Tỉ số đồng dạng)
\( \Rightarrow AC.AE = AD.AH\)
