Hoạt động2
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A’} = \widehat A = 90^\circ ,\,\,\widehat {B’} = \widehat B\) (Hình 84). Chứng minh \(\Delta A’B’C’ \backsim \Delta ABC\).
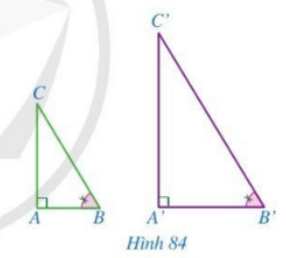
Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba.
Xét tam giác A’B’C’ và tam giác ABC có:
\(\widehat {A’} = \widehat A,\,\,\widehat {B’} = \widehat B\)
\( \Rightarrow \Delta A’B’C’ \backsim \Delta ABC\) (g-g)
Luyện tập2
Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\).
- Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác EHA và DHB đồng dạng.
- Suy ra tỉ số đồng dạng tương ứng.
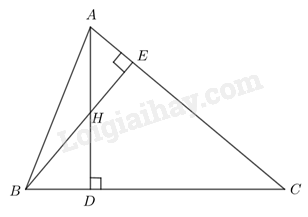
Xét tam giác EHA và tam giác DHB có:
\(\widehat {EHA} = \widehat {DHB}\) (đối đỉnh)
\(\widehat {AEH} = \widehat {BDH} = 90^\circ \)
\( \Rightarrow \Delta EHA \backsim \Delta DHB\) (g-g)
\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (Tỉ số đồng dạng)
\( \Rightarrow HA.HD = HB.HE\)