Từ các đường song song, suy ra các tỉ số bằng với \(\frac{{MN}}{{BC}}\) và \(\frac{{NP}}{{AB}}\) rồi thay vào biểu thức cần chứng minh. Hướng dẫn giải bài 3 trang 94 SGK Toán 8 – Cánh diều Bài tập cuối chương 8. Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC...
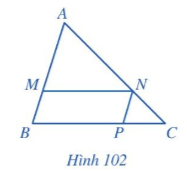
Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = 1\).
Từ các đường song song, suy ra các tỉ số bằng với \(\frac{{MN}}{{BC}}\) và \(\frac{{NP}}{{AB}}\) rồi thay vào biểu thức cần chứng minh.
Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (hệ quả của định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)