
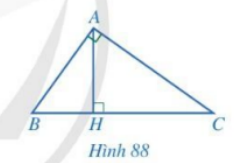
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\)
b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\)
c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\)
d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)

Chứng minh các cặp tam giác đồng dạng rồi suy ra tỉ số đồng dạng tương ứng.

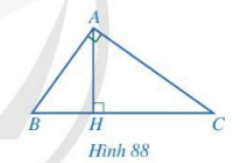
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ ;\,\,\widehat B\) chung
Advertisements (Quảng cáo)
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{AB}}{{HB}} = \frac{{BC}}{{BA}} \Rightarrow A{B^2} = BC.HB\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HAC\) (g-g)
\( \Rightarrow \frac{{AC}}{{HC}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = BC.CH\)
c) Ta có: \(\Delta ABC \backsim \Delta HBA\) và \(\Delta ABC \backsim \Delta HAC\) nên \(\Delta ABH \backsim \Delta CAH\)
\( \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}} \Rightarrow A{H^2} = BH.CH\)
d) Ta có:
\(A{B^2} = BC.BH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.BH}}\)
\(A{C^2} = BC.CH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.CH}}\)
\(A{H^2} = BH.CH \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{BH.CH}}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BC.BH}} + \frac{1}{{BC.CH}}\\ = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right)\\ = \frac{1}{{BC}}.\frac{{BH + CH}}{{BH.CH}}\\ = \frac{1}{{BC}}.\frac{{BC}}{{BH.CH}}\\ = \frac{1}{{BH.CH}}\\ = \frac{1}{{A{H^2}}}\end{array}\)
