Phân tích và lời giải bài 9.42 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức Bài tập cuối chương 9. Cho hình 9. 74, biết rằng . Chứng minh rằng ΔABD∽ΔACE và ΔBOE∽ΔCOD :
Cho hình 9.74, biết rằng \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\). Chứng minh rằng ΔABD∽ΔACE và ΔBOE∽ΔCOD
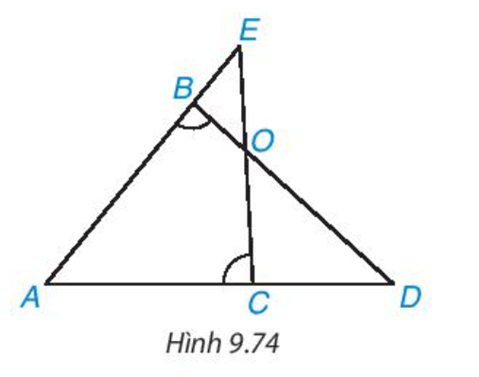
Chứng minh ΔBOE và ΔCOD có: \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) và \(\widehat {EBO} = \widehat {DCO}\)
- Xét tam giác ABD và tam giác ACE có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\), góc A chung
=> ΔABD ∽ ΔACE (g.g)
Advertisements (Quảng cáo)
- Vì ΔABD ∽ ΔACE
=> \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C}\)
=> \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) (1)
- Có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\)
Mà \(\widehat {AB{\rm{D}}} + \widehat {EBO} = {180^o}\)
\(\widehat {AC{\rm{E}}} + \widehat {DCO} = {180^o}\)
=> \(\widehat {EBO} = \widehat {DCO}\) (2)
Từ (1) và (2) => ΔBOE ∽ ΔCOD (g.g)