Hoạt động2
Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC.
- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau
- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN=BP và suy ra \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng

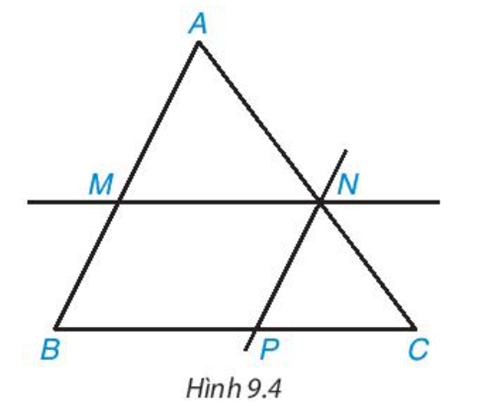
Quan sát hình 9.4 để thực hiện các hoạt động.

- Các cặp góc bằng nhau của hai tam giác ABC và AMN: \(\widehat B = \widehat M{,^{}}\widehat C = \widehat N\)
- Có MN // BP, MB // NP (vì AB // NP) => MN=BP \( \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\)=> ΔABC \(\backsim\) ΔAMN
Luyện tập2
Trong hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.
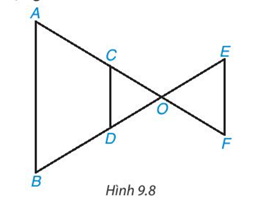

Quan sát hình 9.8 để kể tên các tam giác đồng dạng

Advertisements (Quảng cáo)
ΔOCD \(\backsim\) ΔOAB
ΔOEF \(\backsim\) ΔODC
ΔOEF \(\backsim\) ΔOBA
Vận dụng
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Hãy giải thích bác Dương đã tính được chiều cao cột đèn như thế nào, biết cọc gỗ cao 1m, EC=80cm và EB=4m.
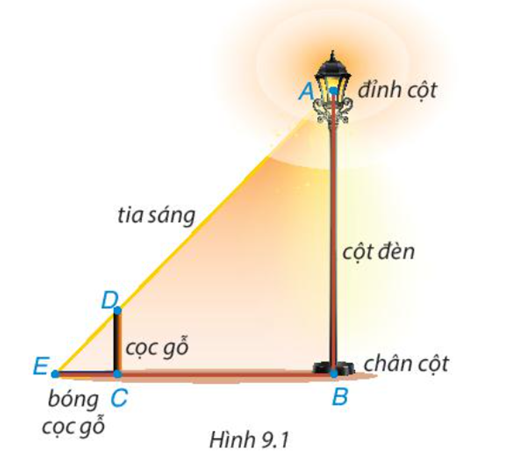

Dựa vào định lí ΔAEB \(\backsim\) ΔDEC và tìm tỉ số đồng dạng của chúng từ đó tính được chiều cao của cột đèn

Có EB=4m=400cm, CD=1m=100cm
Vì cọc gỗ và cột đèn đều thẳng đứng
=> AB // DC => ΔAEB \(\backsim\) ΔDEC
\( \Rightarrow \frac{{DE}}{{A{\rm{E}}}} = \frac{{CE}}{{BE}} = \frac{{DC}}{{AB}}\)
Mà \(\frac{{CE}}{{A{\rm{E}}}} = \frac{{80}}{{100}} = \frac{1}{5}\)
=> Hai tam giác đồng dạng với tỉ số đồng dạng là \(\frac{1}{5}\)
\( \Rightarrow \frac{{DC}}{{AB}} = \frac{{100}}{{AB}} = \frac{1}{5}\)
=> AB=500cm=5m
Vậy cột đèn cao 5m
