1. Nhân hai phân thức
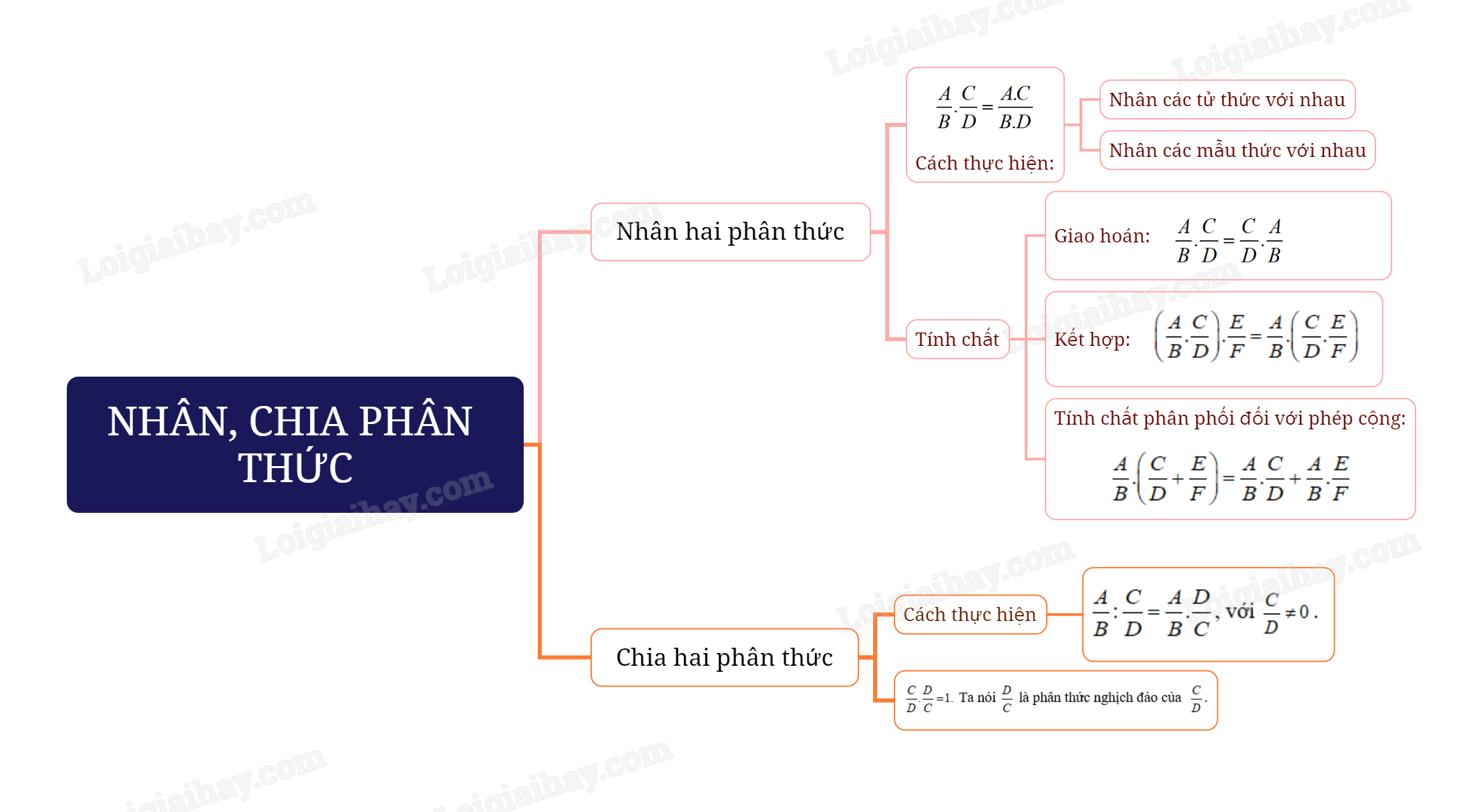
Quy tắc: Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau.
\(\frac{A}{B}.\frac{C}{D} = \frac{{A.C}}{{B.D}}\)
Chú ý: Kết quả của phép nhân hai phân thức được gọi là tích. Ta thường viết tích dưới dạng rút gọn.
2. Tính chất của phép nhân phân thức
- Giao hoán: \(\frac{A}{B}.\frac{C}{D} = \frac{C}{D}.\frac{A}{B}\)
- Kết hợp: \(\left( {\frac{A}{B}.\frac{C}{D}} \right).\frac{E}{F} = \frac{A}{B}.\left( {\frac{C}{D}.\frac{E}{F}} \right)\)
- Tính chất phân phối đối với phép cộng: \(\frac{A}{B}.\left( {\frac{C}{D} + \frac{E}{F}} \right) = \frac{A}{B}.\frac{C}{D} + \frac{A}{B}.\frac{E}{F}\)
Ví dụ:
\(\frac{{2xz}}{{3y}}.\frac{{ - 6{y^3}}}{{8{x^2}z}} = \frac{{2xz.( - 6{y^3})}}{{3y.8{x^2}z}} = \frac{{ - {y^2}}}{{2x}}\);
\(\frac{{{x^2} - 1}}{{{x^2} + 4x}}.\frac{{2x}}{{x - 1}} = \frac{{(x - 1)(x + 1).2x}}{{x(x + 4)(x - 1)}} = \frac{{2(x + 1)}}{{x + 4}}\)
Advertisements (Quảng cáo)
3. Chia hai phân thức
Quy tắc: Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\) khác 0, ta nhân phân thức \(\frac{A}{B}\) với phân thức \(\frac{D}{C}\):
\(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C}\), với \(\frac{C}{D} \ne 0\).
Nhận xét: \(\frac{C}{D}.\frac{D}{C} = 1.\) Ta nói \(\frac{D}{C}\) là phân thức nghịch đảo của \(\frac{C}{D}\).
Ví dụ:
1)
\(\frac{{{x^2} - 9}}{{x - 2}}:\frac{{x - 3}}{x} \\= \frac{{(x - 3)(x + 3)}}{{x - 2}}.\frac{x}{{x - 3}} \\= \frac{{(x - 3)(x + 3).x}}{{(x - 2)(x - 3)}} \\= \frac{{x(x + 3)}}{{x - 2}}\)
2)
\(\frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}:\frac{{{x^3}}}{{yz}} \\= \frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}.\frac{{yz}}{{{x^3}}} \\= \frac{{x.xz.yz}}{{{z^2}.{y^3}.{x^3}}} \\= \frac{{{x^2}y{z^2}}}{{{x^3}{y^3}{z^2}}} \\= \frac{1}{{x{y^2}}}\)