Bài 37 trang 130 sgk Toán 8 tập 1, Bài 37. Thực hiện các phép đo cần thiết( chính xác đến từng mm) để tính diện tích hình ABCDE (h.152)...

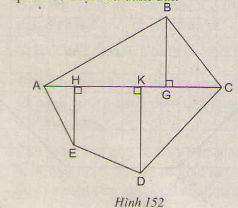
Bài 37. Thực hiện các phép đo cần thiết( chính xác đến từng mm) để tính diện tích hình ABCDE (h.152).

 Hướng dẫn giải:

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.

Thực hiện phép đo chính xác đến mm ta được:

BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm

KC = 22mm, EH = 16mm, KD = 23mm

Nên  S_ABC  = \(\frac{1}{2}\).BG. AC = \(\frac{1}{2}\) 19.48 = 456 (mm²)

 S_AHE  = \(\frac{1}{2}\) AH. HE = \(\frac{1}{2}\) 8.16 = 64 (mm²)

S_DKC  = \(\frac{1}{2}\) KC.KD = \(\frac{1}{2}\) 22.23 = 253(mm²)

S_HKDE = \(\frac{\left ( HE+KD \right ).HK}{2}\) = \(\frac{\left (16+23 \right ).18}{2}\)= 351 (mm²)

Do đó 

S_ABCDE = S_ABC + S_AHE + S_DKC + S_HKDE = 456 + 64 + 253+ 351

Vậy S_ABCDE = 1124(mm²)