1. Định nghĩa
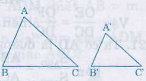
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
\(\widehat{A'}\) = \(\widehat{A}\); \(\widehat{B'}\) = \(\widehat{B}\); \(\widehat{C'}\)= \(\widehat{C}\).
\(\frac{A'B'}{AB}\) = \(\frac{B'C'}{BC}\) = \(\frac{C'A'}{CA}\)
Kí hiệu: ∆A’B’C’ ~ ∆ABC
Tỉ số: \(\frac{A'B'}{AB}\) = \(\frac{B'C'}{BC}\) = \(\frac{C'A'}{CA}\) = k gọi là tỉ số đồng dạng.
2. Tính chất
Hai tam giác A’B’C’ và ABC đồng dạng có một số tính chất:
Advertisements (Quảng cáo)
1) ∆ABC ~ ∆A’B’C’
2) Nếu ∆A’B’C’ ~ ∆ABC thì ∆ABC ~ ∆A’B’C’
3) Nếu ∆A’B’C’ ~ ∆A”B”C” và ∆A”B”C” ~ ∆ABC thì ∆A’B’C’ ~ ∆ABC
3 . Định lí
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

4. Chú ý
Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài của hai tam giác song song với cạnh còn lại.
