Áp dụng định lí Pythagore để tính độ dài trung đoạn. Sau đó sử dụng công thức tính diện tích xung quanh của hình chóp. Giải và trình bày phương pháp giải Giải bài 5 trang 112 vở thực hành Toán 8 tập 2 - Bài 38. Hình chóp tam giác đều . Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng 10cm, cạnh đáy bằng 12 cm. (H.10.7).
Câu hỏi/bài tập:

Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng 10cm, cạnh đáy bằng 12 cm. (H.10.7). Tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
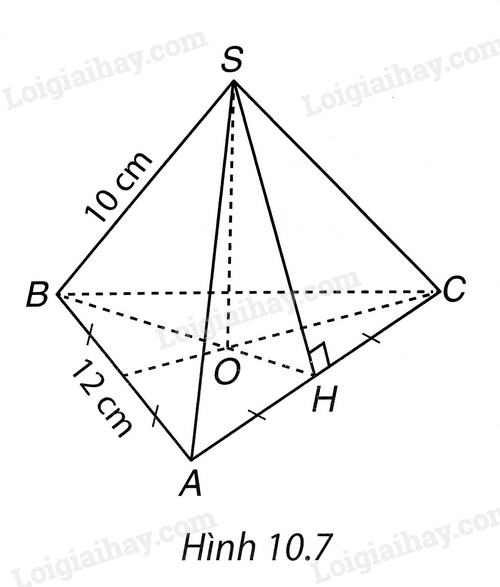

Áp dụng định lý Pythagore để tính độ dài trung đoạn. Sau đó sử dụng công thức tính diện tích xung quanh của hình chóp tam giác để tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
Advertisements (Quảng cáo)

AH = 6cm. \(\Delta SAH\) vuông tại H nên theo định lý Pythagore ta có SH2 + AH2 = SA2.
SH2 + 622 = 102
SH2 = 102 – 62 = 82
Suy ra SH = 8 (cm)
Diện tích xung quanh của hình chóp là: \({S_{xq}} = p.d = \frac{{12.3}}{2}.8 = 144\left( {c{m^2}} \right)\).
