Sử dụng tính chất đường trung bình của tam giác. Chứng minh EDKI là hình bình hành suy ra EI = DK. Phân tích, đưa ra lời giải Giải bài 5 trang 74 vở thực hành Toán 8 - Bài 16. Đường trung bình trong tam giác . Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G.
Câu hỏi/bài tập:

Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng EI = DK.

- Sử dụng tính chất đường trung bình của tam giác.
- Chứng minh EDKI là hình bình hành suy ra EI = DK.

Advertisements (Quảng cáo)
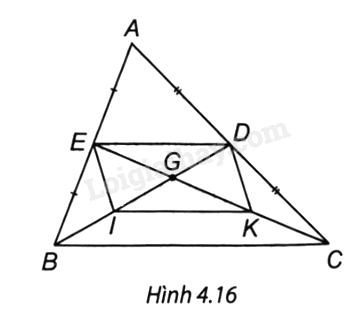
∆ABC có: E là trung điểm AB, D là trung điểm AC, nên DE là đường trung bình của ∆ABC.
Suy ra ED // BC và \(ED = \frac{1}{2}BC\) (tính chất đường trung bình của tam giác). (1)
∆GBC có: I là trung điểm GB, K là trung điểm GC nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và \(IK{\rm{ }} = \frac{1}{2}BC\). (2)
Từ (1) và (2) suy ra: IK // ED, IK = ED.
Tứ giác EDKI có: IK // ED, IK = ED nên tứ giác EDKI là hình bình hành.
Suy ra EI = DK.
