Chọn phương án đúng trong mỗi câu sau:
Câu 1 trang 75
Quan sát Hình 4.17 và chọn khẳng định đúng.
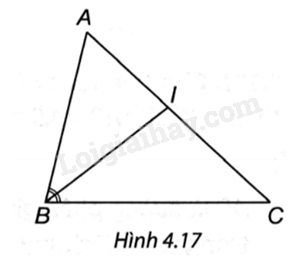
A. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{AC}}.\)
B. \(\frac{{IA}}{{IC}} = \frac{{BC}}{{BA}}.\)
C. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{BC}}.\)
D. \(\frac{{IA}}{{IC}} = \frac{{AC}}{{AB}}.\)

Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

Ta có IB là đường phân giác của góc B nên \(\frac{{IA}}{{IC}} = \frac{{AB}}{{BC}}.\)
=> Chọn đáp án C.
Câu 2 trang 75
Quan sát Hình 4.18, biết BI là phân giác của góc B, AB = 12 cm, BC = 15 cm, AC = 9 cm. Độ dài đoạn IA là:
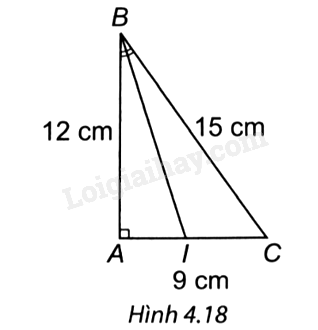
A. 5 cm.
B. 4 cm.
C. 6 cm.
D. 3 cm.

Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

Ta có BI là phân giác của góc B nên
\(\frac{{IA}}{{AB}} = \frac{{IC}}{{BC}} = \frac{{IA + IC}}{{AB + BC}} = \frac{{AC}}{{AB + BC}} = \frac{9}{{12 + 15}} = \frac{9}{{27}} = \frac{1}{3}\)
Do đó \(IA = \frac{1}{3} \cdot AB = \frac{1}{3} \cdot 12 = 4\) (cm).
=> Chọn đáp án B.
Advertisements (Quảng cáo)
Câu 3 trang 76
Quan sát Hình 4.19. Tỉ số \(\frac{x}{y}\) bằng
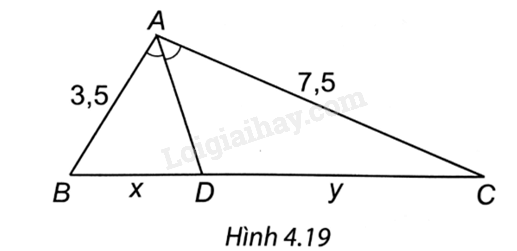
A. \(\frac{1}{7}\).
B. \(\frac{{15}}{7}\)
C. \(\frac{7}{{15}}\)
D. \(\frac{2}{{15}}\)

Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Do đó \(\frac{x}{y} = \frac{{3,5}}{{7,5}} = \frac{7}{{15}}.\)
=> Chọn đáp án C.
Câu 4 trang 76
Quan sát Hình 4.20. Độ dài x, y lần lượt là:
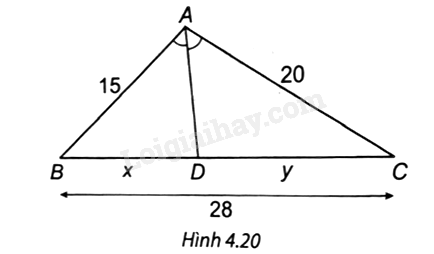
A. x = 16 cm; y = 12 cm.
B. x = 14 cm; y = 14 cm.
C. x = 14,3 cm; y = 10,7 cm.
D. x = 12 cm; y = 16 cm.

Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Khi đó \(\frac{x}{{15}} = \frac{y}{{20}} = \frac{{x + y}}{{15 + 20}} = \frac{{28}}{{35}} = \frac{4}{5}\).
Do đó \(x = \frac{4}{5} \cdot 15 = 12\,\,\left( {cm} \right);y = \frac{4}{5} \cdot 20 = 16\,\,\left( {cm} \right).\)
=> Chọn đáp án D.
