Câu hỏi/bài tập:

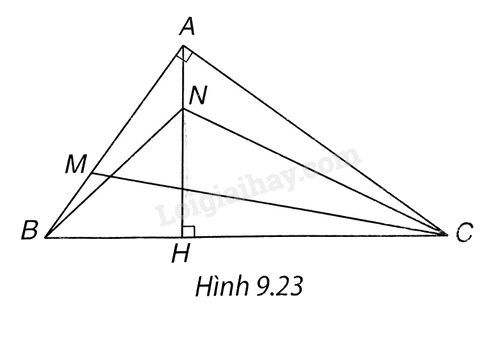
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là các điểm trên các đoạn thẳng AB, AH sao cho AM = 2.MB, AN = $\frac{1}{2}$NH.
Chứng minh rằng $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$.

Chứng minh \(\Delta CAH\backsim \Delta CBA\) => $\frac{CA}{CB}=\frac{AH}{BA}=\frac{AN}{CA}$ và $\widehat{CAH}=\widehat{CBA}$.
Chứng minh $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$ dựa vào tỉ số cạnh tương ứng và góc xen giữa bằng nhau.

Advertisements (Quảng cáo)
(H.9.23). Hai tam giác vuông CAH (vuông tại H) và CBA (vuông tại A) có góc C chung. Do đó \(\Delta CAH\backsim \Delta CBA\) (một cặp góc nhọn bằng nhau).
Suy ra $\frac{CA}{CB}=\frac{AH}{BA}=\frac{AN}{CA}$ và $\widehat{CAH}=\widehat{CBA}$.
Hai tam giác CAN và CBM có:
$\frac{CA}{CB}=\frac{AN}{BM}$ (theo chứng minh trên),
$\widehat{CBM}=\widehat{CAH}=\widehat{CBA}=\widehat{CBN}$ (theo chứng minh trên).
Vậy $\Delta CAN\backsim \Delta CBM$ (c.g.c).
Hai tam giác vuông CHN (vuông tại H) và CAM (vuông tại A) có:
$\frac{HC}{AC}=\frac{HA}{AB}=\frac{HN}{AM}$ (vì $\Delta CAH\backsim \Delta CBA$).
Vậy $\Delta CHN\backsim \Delta CAM$ (cạnh góc vuông – cạnh góc vuông)
