Câu hỏi/bài tập:

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi H là trung điểm của OB, K là trung điểm của OD
a) Hỏi tứ giác AHCK là hình gì?
b) Hình bình hành ABCD phải thỏa mãn điều kiện gì để tứ giác AHCK là:
- Một hình thoi
- Một hình chữ nhật
- Một hình vuông

Vẽ hình theo yêu cầu của đề bài
Advertisements (Quảng cáo)
a) Chứng minh tứ giác AHCK có hai đường chéo cắt nhau tại trung diểm của mỗi đường nên AHCK là hình bình hành.
b) Để tứ giác AHCK là một hình thoi thì hình bình hành ABCD phải là hình thoi
Để tứ giác AHCK là một hình chữ nhật thì hình bình hành ABCD có đường chéo BD dài gấp 2 lần đường chéo AC.
Để tứ giác AHCK là một vuông thì hình bình hành ABCD phải là hình thoi, đường chéo BD dài gấp 2 lần đường chéo AC.

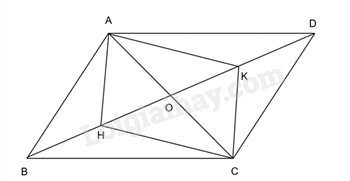
a) Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Do H và K lần lượt là trung điểm của OB và OD nên \(OH = \frac{{OB}}{2} = \frac{{OD}}{2} = OK\).
Các kết quả trên cho thấy tứ giác AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường. Vậy tứ giác AHCK là hình bình hành.
b)
- Muốn tứ giác AHCK là hình thoi, ta cần thêm điều kiện hai đường chéo AC và HK vuông góc với nhau, cũng có nghĩa là AC \( \bot \) BD. Điều này xảy ra khi ABCD là hình thoi. Vậy điều kiện để tứ giác AHCK là hình thoi là tứ giác ABCD là hình thoi.
- Muốn tứ giác AHCK là hình chữ nhật, ta cần thêm điều kiện hai đường chéo AC và HK bằng nhau, tức là AC = HK. Do H và K lần lượt là trung điểm của OB và OD nên điều kiện đó cũng có nghĩa là \(AC = \frac{1}{2}BD\). Vậy điều kiện để tứ giác AHCK là hình chữ nhật là ABCD có đường chéo BD dài gấp 2 lần đường chéo AC.
- Tứ giác AHCK là hình vuông khi nó vừa là hình thoi, vừa là hình chữ nhật.
- Do đó, theo kết quả hai câu trên, để AHCK là một hình vuông, thì hình bình hành ABCD phải là hình thoi, đường chéo BD dài gấp 2 lần đường chéo AC.
